FFT Benchmark in MaixPy on Sipeed Maix Bit

We ran an FFT benchmark in the MaixPy on the Sipeed’s Maix Bit featuring the Kendryte K210.
The result is a little strange.
In this article, the MaixPy function using the FFT accelerator is called Hard FFT, and the ulab FFT function built into the MaixPy is called Soft FFT or ulab FFT.

Sipeed Maix Bit

The Maix Bit is a low-cost development board from Sipeed, featuring the Kendryte K210 from Canaan.
The Kendryte K210 is an SoC that includes:

• Dual-core 64-bit RISC-V,
• KPU (Knowledge Processing Unit),
• APU (Audio Processing Unit),
• FFT (Fast Fourier Transform) accelerator,
• etc.

MaixPy

MaixPy is a MicroPython for the Sipeed’s Maix series with Kendryte K210.
In this article, we used the maixpy_v0.6.2_46_geafab8cfd.bin.

Benchmark of Hard FFT

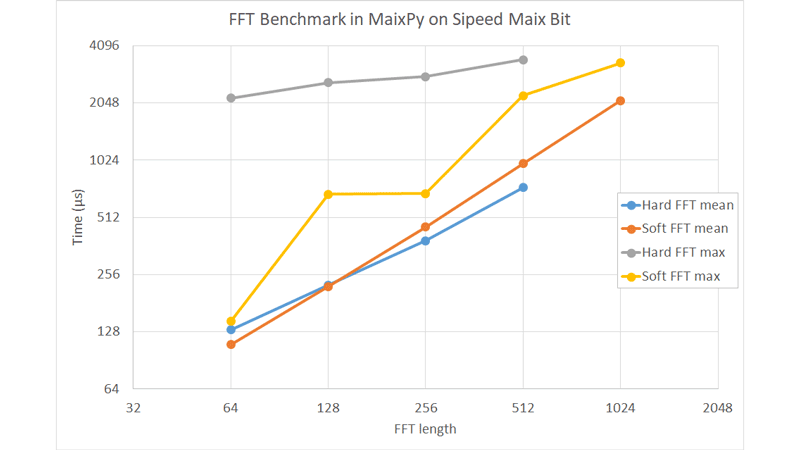
The Hard FFT benchmark results are as follows.

FFT length	Time (us)
	mean	std	min	max
64	130.88	205.17	105	2165
128	225.04	325.70	172	2616
256	386.18	400.60	305	2819
512	735.62	591.07	570	3449

The difference between the mean and max of the processing time is large, and this effect appears in the standard deviation (std).

Benchmark of Soft FFT

The ulab FFT benchmark results are as follows.

FFT length	Time (us)
	mean	std	min	max
64	109.51	5.20	107	145
128	221.36	46.26	214	677
256	455.62	25.70	447	683
512	979.89	128.39	956	2231
1024	2109.83	174.96	2059	3317

Since the RISC-V of K210 has an FPU, the processing time is the same as that of the Hard FFT.
Also, although the max time fluctuates slightly, the std is less than 1/3 of the mean.
In addition, MaixPy ulab FFT uses FP32.

Summary

We ran an FFT benchmark in the MaixPyon on the Sipeed Maix Bit.
We found the following.

• The processing time of the Hard FFT fluctuates greatly.
• The mean processing time of the Soft FFT is the same as that of the Hard FFT.