GEMM based on the RISC-V Vector Extension (Part 3)
We will describe several times floating-point matrix multiplication kernels based on the RISC-V Vector Extension. In Part 3, we completed a GEMM that supports transposed matrix, alpha and beta, and evaluated its performance using Ara’s RTL simulator.
In Part 1 of the related article, we evaluate the performance of double-, single- and half-precision floating-point matrix multiplication kernels for arbitrary matrix sizes. Also, in Part 2, we evaluate vector load/store performance for transposed matrix support.
Goal
Here we revisit the main points of the goal set in Part 1.
The goal is to create floating-point matrix multiplication kernels based on the RISC-V Vector Extension and evaluate their performance using Ara’s RTL simulator.
Specifically, it targets GEMM (GEneral Matrix-to-matrix Multiply) compatible matrix multiplication kernels for BLAS (Basic Linear Algebra Subprograms).
The processing is as follows.
C = alpha * op(A) * op(B) + beta * C with op(A) = [M x K], op(B) = [K x N], C = [M x N]
op(A) uses A as is when TransA is N, and uses transposed A when TransA is not N. The same is true for op(B).
Implementation of GEMM
Here we will look at the implementation of GEMM in Part 3.
The prototype declaration of the single-precision floating-point matrix multiplication kernel SGEMM implemented in Part 1 was as follows. As of Part 1, transposed matrix, alpha and beta are not supported.
// C = A * B
void sgemm(const CBLAS_INT M,
const CBLAS_INT N,
const CBLAS_INT K,
const float* A,
const CBLAS_INT lda,
const float* B,
const CBLAS_INT ldb,
float* C,
const CBLAS_INT ldc);
The prototype declaration of SGEMM implemented in Part 3 is as follows. Transposed matrix, alpha and beta are supported, and we can see that it is GEMM compatible, which is our goal.
// C = alpha * op(A) * op(B) + beta * C
void sgemm(CBLAS_TRANSPOSE TransA,
CBLAS_TRANSPOSE TransB,
const CBLAS_INT M,
const CBLAS_INT N,
const CBLAS_INT K,
const float alpha,
const float* A,
const CBLAS_INT lda,
const float* B,
const CBLAS_INT ldb,
const float beta,
float* C,
const CBLAS_INT ldc);
The processing flow of the implemented GEMM is expressed in pseudocode as follows.
// C = alpha * op(A) * op(B) + beta * C
// 1st block (C = beta * C)
if (beta != 1.0) {
if (beta == 0.0) {
C = 0.0
} else {
C = beta * C
}
}
// 2nd block (AB = op(A) * op(B))
if (TransB != 'N') {
// AB = A * Bt
Bt = transpose(B)
if (TransA != 'N') {
AB = matmul_tn(A, Bt)
} else {
AB = matmul_nn(A, Bt)
}
} else {
// AB = A * B
if (TransA != 'N') {
AB = matmul_tn(A, B)
} else {
AB = matmul_nn(A, B)
}
}
// 3rd block
C = alpha * AB + C
The processing of the implemented GEMM is divided into three blocks. The first and second blocks perform operations on C = beta * C and AB = op(A) * op(B) respectively. The third block computes C using alpha and the results of the first and second blocks.
In the second block, as described in Part 2, if the transposition of matrix B is required, in order to reduce the use of stride load instructions, the transposed matrix BT, Bt in pseudocode, is created in advance.
GEMM on Ara RTL Simulator
Here, we will look at the performance of the implemented GEMM using Ara’s RTL simulator.
First, we consider the number of floating-point operations (FLOPs) in GEMM, which we implemented in Part 3. The number of FLOPs of the implemented GEMM changes according to the beta value of the first block. For this reason, only the number of FLOPs in the 2nd and 3rd blocks is of interest. The number of FLOPs for A * B in the second block is 2MNK as in Part 1 implementation. The number of FLOPs for C = alpha * AB + C in the third block is 2MN because the number of multiplications and additions for MN elements of the matrix C is performed. As a result, the number of FLOPs for the implemented GEMM is at least 2MNK + 2MN. Performance is calculated using this number of FLOPs.
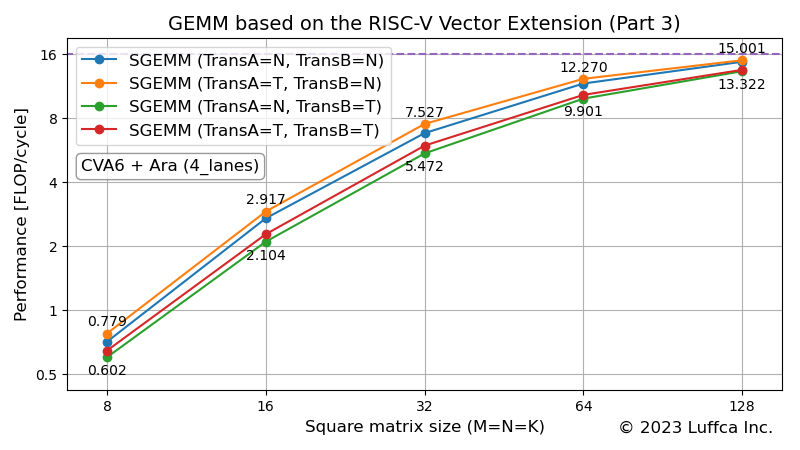
The featured image shows the performance (FLOP/cycle) of SGEMM in Ara’s 4_lanes (256-bit vector operation width with four 64-bit Vector Units) configuration. N and T representing the settings of TransA and TransB correspond to no transposition and transposition, respectively.
Also, the dashed line with a performance of 16 in the featured image represents the roofline. Ara’s Vector Unit is equipped with FMA (Fused Multiply-Add), which supports 16 single-precision floating-point operations per cycle even with a 256-bit vector operation width configuration.
The table below shows the performance and utilization of SGEMM when the size of the square matrix (M=N=K) is 128.
| Performance (FLOP/cycle) |
Utilization (%) |
|
|---|---|---|
| SGEMM (TransA=N, TransB=N) | 14.756 | 92.2 |
| SGEMM (TransA=T, TransB=N) | 15.001 | 93.8 |
| SGEMM (TransA=N, TransB=T) | 13.322 | 83.3 |
| SGEMM (TransA=T, TransB=T) | 13.521 | 84.5 |
It can be seen that the utilization of the group with TransB=N is 92-93% and the utilization of the group with TransB=T is 83-84%.
Utilization is the value obtained by dividing the performance by the theoretical performance. In Ara with a vector operation width of 256-bit, the theoretical performance of single-precision floating-point operations per cycle is 16, so the utilization (%) of SGEMM (TransA=T, TransB=N) is 15.001 / 16 * 100 = 93.8.
Analysis of results
Support for transposed matrix
From the table above, we can see that SGEMM (TransA=T, TransB=N) has the highest utilization and SGEMM (TransA=N, TransB=T) has the lowest utilization. Here we analyze this result.
A closer look at the table shows that the TransB=T group is less efficient than the TransB=N group. The reason for this is that, as described in Part 2, when transposing matrix B is necessary, we chose to pre-create the transposed matrix BT in order to reduce the use of strided accesses, which have low performance. When the square matrix size is 128, it takes about 30k cycles to create the transposed matrix BT, so the utilization drops by about 9%.
If the square matrix size is n, the number of cycles required to create the transposed matrix BT is proportional to n2, while the amount of matrix multiplication is proportional to n3. Therefore, as the matrix size increases, the utilization of the group TransB=T approaches the utilization of the group TransB=N.
Contrary to the TransB=T group above, the TransA=N group is slightly (1.2-1.5%) less efficient than the TransA=T group. This is also due to stride access, just like the matrix B. However, for the matrix A, continuous access occurs when TransA=T, and stride access occurs when TransA=N. Also, for the matrix A, the number of elements loaded in the innermost loop is small, and the elements are loaded by the load instructions of the processor CVA6 instead of the vector load instructions of Ara.
These are the reasons why SGEMM (TransA=T, TransB=N) has the highest utilization and SGEMM (TransA=N, TransB=T) has the lowest utilization. Note that the implementation of GEMM in Part 1-3 assumes row-major matrices. For column-major matrices, contrary to our results, SGEMM (TransA=N, TransB=T) is the most efficient, and SGEMM (TransA=T, TransB=N) is the least efficient.
Support for alpha and beta
Here we look at the impact of alpha and beta support.
The SGEMM in Part 1, which does not support alpha and beta, has an utilization of 96.5% when the square matrix size is 128. The utilization of the SGEMM (TransA=N, TransB=N) implemented in Part 3 is 92.2%, which is 4.3% less efficient.
The reason for this is thought to be that Ara’s AXI data width is set to half the vector operation width.
Even if the AXI data width is half the vector operation width, memory access can be hidden if the number of elements for vector operation is more than twice the number of elements to be loaded, as in the second block of this implementation.
On the other hand, if the number of load/store elements is equal to or greater than the number of vector operation elements, such as C = beta * C in the first block or C = alpha * AB + C in the third block, the number of cycles for load/store becomes the critical path and utilization drops.
Summary
We have created a GEMM-compatible floating-point matrix multiplication kernel based on the RISC-V Vector Extension and evaluated its performance using Ara’s RTL simulator.
