GEMM based on the RISC-V Vector Extension (Part 2)
We will describe several times floating-point matrix multiplication kernels based on the RISC-V Vector Extension. In Part 2, we have evaluated vector load/store performance to support transposed matrix using Ara’s RTL simulator.
In the related article, GEMM based on the RISC-V Vector Extension (Part 1), we have evaluated the performance of double-, single- and half-precision floating-point matrix multiplication kernels for arbitrary matrix sizes.
Vector Loads and Stores
The RISC-V Vector Extension has the following vector load/store instructions for moving values between vector registers and memory.
- Vector Unit-Stride Instructions
- Vector Strided Instructions
- Vector Indexed Instructions
- Vector Unit-Stride Fault-Only-First Loads
- Vector Load/Store Segment Instructions
This article describes vector unit-stride instructions for consecutive accesses and vector strided instructions for strided accesses.
Vector Unit-Stride Instructions
Vector unit-stride instructions move values between consecutive data in memory and vector registers.
# Vector unit-stride loads and stores # vd destination, rs1 base address, vm is mask encoding (v0.t or <missing>) vle8.v vd, (rs1), vm # 8-bit unit-stride load vle16.v vd, (rs1), vm # 16-bit unit-stride load vle32.v vd, (rs1), vm # 32-bit unit-stride load vle64.v vd, (rs1), vm # 64-bit unit-stride load # vs store data, rs1 base address, vm is mask encoding (v0.t or <missing>) vse8.v vs, (rs1), vm # 8-bit unit-stride store vse16.v vs, (rs1), vm # 16-bit unit-stride store vse32.v vs, (rs1), vm # 32-bit unit-stride store vse64.v vs, (rs1), vm # 64-bit unit-stride store
In the example below, vl consecutive 32-bit values from address a are loaded into vector registers v0 and v1.
float* a;
asm volatile("vsetvli %0, %1, e32, m2, ta, ma" : "=r"(vl) : "r"(n));
asm volatile("vle32.v v0, (%0)" ::"r"(a));
Vector Strided Instructions
Vector strided instructions move values between spaced intervals of data in memory and vector registers.
# Vector strided loads and stores # vd destination, rs1 base address, rs2 byte stride vlse8.v vd, (rs1), rs2, vm # 8-bit strided load vlse16.v vd, (rs1), rs2, vm # 16-bit strided load vlse32.v vd, (rs1), rs2, vm # 32-bit strided load vlse64.v vd, (rs1), rs2, vm # 64-bit strided load # vs store data, rs1 base address, rs2 byte stride vsse8.v vs, (rs1), rs2, vm # 8-bit strided store vsse16.v vs, (rs1), rs2, vm # 16-bit strided store vsse32.v vs, (rs1), rs2, vm # 32-bit strided store vsse64.v vs, (rs1), rs2, vm # 64-bit strided store
In the example below, vl 32-bit values spaced n from address a are loaded into vector registers v0 and v1.
float* a;
asm volatile("vsetvli %0, %1, e32, m2, ta, ma" : "=r"(vl) : "r"(m));
asm volatile("vlse32.v v0, (%0), %1" ::"r"(a), "r"(n * sizeof(float)));
Vector Load/Store on Ara RTL Simulator
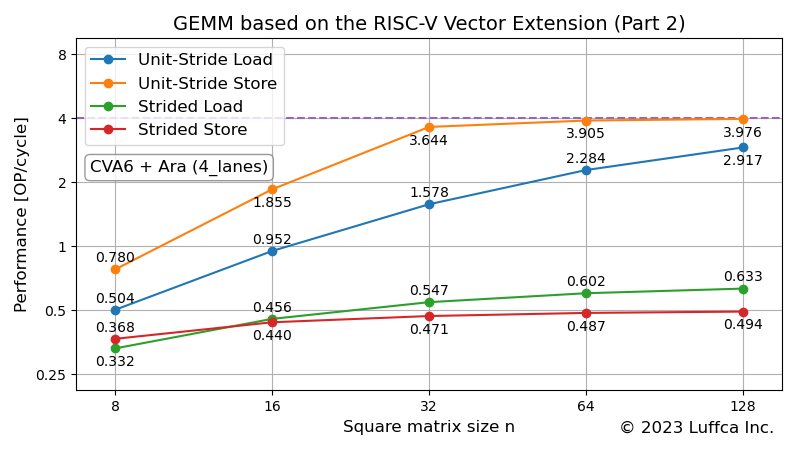
Featured image shows the performance of 32-bit unit-stride load/store (vle32.v and vse32.v) and strided load/store (vlse32.v and vsse32.v) in 4_lanes configuration of Ara’s RTL simulator.
Note that the AXI data width for Ara’s 4_lanes configuration is 128-bit, so the roofline for 32-bit data is 4.
It can be seen that the unit-stride load/store performance is asymptotic to the roofline, while the strided load/store performance is poor. When the square matrix size is 128, the performance of strided load/store is about 1/4 and 1/8 of that of unit-stride load/store, respectively.
GEMM transposed matrix support
Here we consider transposed matrix support for GEMM (GEneral Matrix-to-matrix Multiply).
Switching the vector load instruction from unit-stride load to strided load is the easiest way to support transposed matrix in GEMM, but the performance is greatly reduced. The vector load instruction is used in the innermost loop of the GEMM. For this reason, switching to strided load, which has lower performance than unit-stride load, reveals previously hidden memory accesses and affects the number of cycles.
In this case, we chose to create a pre-transposed matrix BT when we need to transpose the matrix B, and then perform unit-stride load from the matrix BT in the innermost loop of the GEMM. This does not degrade the performance of the innermost loop of GEMM, and strided access is only used when creating matrix BT.
There are two possible ways to create the matrix BT using the vector load/store instructions.
- Method 1: Strided store after unit-stride load
- Method 2: Unit-stride store after strided load
Comparing the two methods based on the individual performance shown in the featured image, method 2 has higher performance, and the same results were obtained in actual measurements. When the square matrix size n is 128, the number of cycles to create a single-precision floating-point matrix BT is approximately 30k (≈2n2).
It is also possible to create the matrix BT using the CVA6 processor, but the performance is about 1/4 of method 2.
Summary
We have evaluated vector load/store performance using Ara’s RTL simulator for transposed matrix support of floating-point matrix multiplication kernels based on the RISC-V Vector Extension.
In Ara, we found that strided access performed poorly compared to sequential access. We chose to create a pre-transposed matrix BT to reduce the number of strided accesses used when we need to transpose the matrix B.